Snowflake

a snowflake simulator

Kenneth Libbrecht at CalTech has done some amazing research on the physics of snowflake formation. The image to the left links to an animated gif showing time-lapse photography of a lab-grown snowlake.

Since viewing the formation of snowflakes in the wild isn't possible currently, I thought an interesting graphics project would be to simulate the growth of snowflakes as they fall.

keys:
  ESC                 - quit
  0   zero            - cycle through 5 "real life" snowflakes
  
  1-5                 - various procedural generators. (described in html)
  
  1                   - 'flower' generator.
  2                   - 'mosaic' generator.
  3                   - 'lineart' generator.
  4                   - 'outside-in (sushi-roll) lineart' generator
  5                   - 'random barycentric triple' generator
  
  R                   - reset generator
  
  A                   - 'auto' camera; smooth rotation around snowflake
  
  []  square brackets - adjust polarization
  <>  angle brackets  - adjust spectrum bias for polarization
  -=  minus/equals    - adjust thickness of interface/refraction factor

mouse:
  LEFT MOUSE DRAG   - rotate the camera
  RIGHT MOUSE DRAG  - rotate the snowflake
  MOUSE WHEEL       - zoom in/out on snowflake

• camera is centered on the snowflake's frame as it forms.
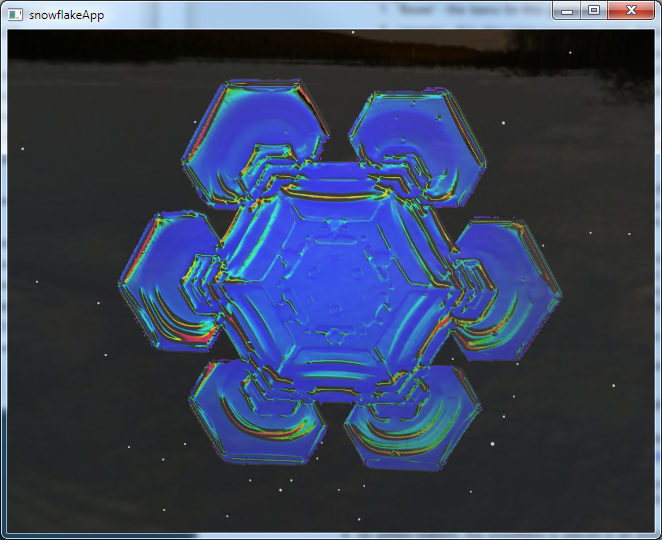
• pressing number keys allow the viewer to switch between generators and real-life snowflakes (from SnowCrystals.com)-- generated snowflakes are random on two parameters and are different each time they are regenerated. There are 5 different generators with varying levels of randomization (no two are the same -- mostly!):
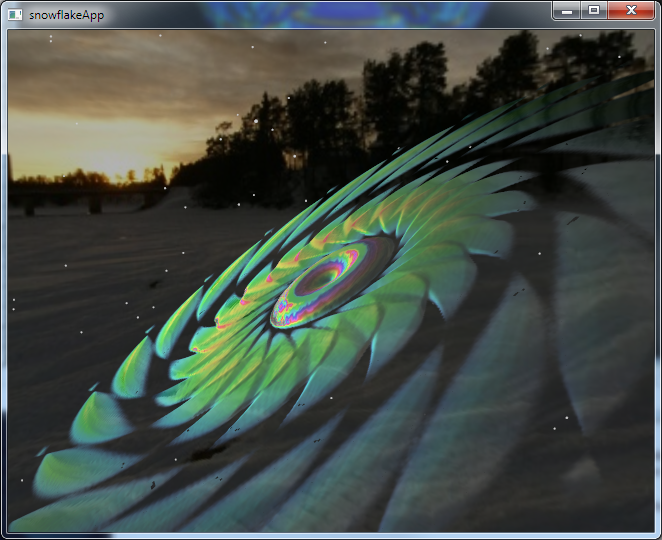
  1. 'flower' - the basis for this generator are rects of sine modulated size that sweep outwards. the effect is like a colorful flower.
  2. 'mosaic' - this also uses sweeping rects, however this time the radial position is modulated so that a mosaic is formed.
  3. 'lineart' - this uses two lines of adjacent symmetry which are then connected each to the midpoint of the other as they expand radially. The connection idea was derived from patterns common in peg-based lineart.
  4. 'outside-in (sushi-roll) lineart' - similar to 'lineart', this reuses the modulated radial expansion in reverse, drawing outside in, and creating fractal like hubs.
  5. 'random barycentric triple' - taking two lines of adjacent symmetry as basis vectors, 3 additional points are constructed using barycentric coordinates. Since the additional points are random points within the radially expanding triangle, this produces different and more complex patterns than 'lineart'.
• "thin-film"/polarized light shading effects -- Rotating the snowflake with respect to the light source produces effects characteristic of thin films. Libbrecht finds that using a color filter (polarized light) (see the section on "Illumination Techniques") brings out the best contrast in his photos. This is a form of thin-film interference as the surfaces of the snowflake are accented by the polarized filter (see nvidia's thinfilm shader or photographs of real crystals via polarized light microscopy).


• 

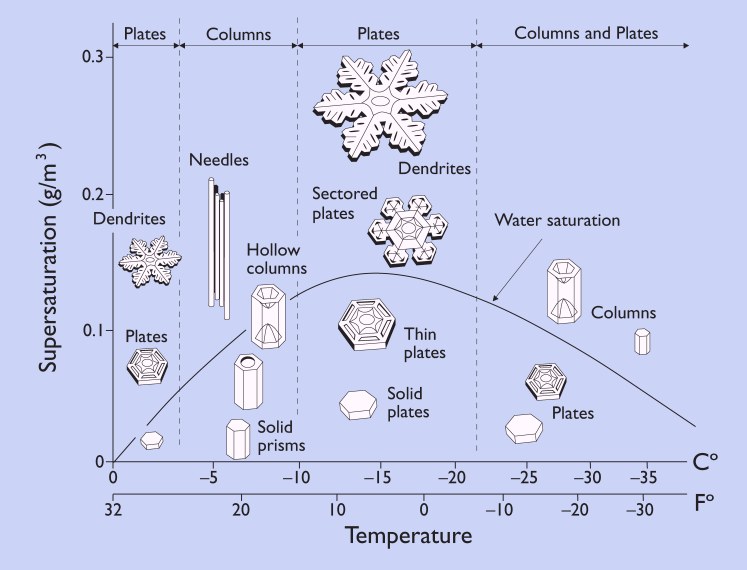
  generative growth simulation -- Libbrecht describes the physics of snowflake formation based on diffusion dynamics within environmental parameters of temperature and humidity. Using the physics to approximate growth is a difficult problem and still not well understood [Libbrecht, Kim]. Unfortunately I was not able to get my diffusion simulation working in the time alloted, so I included a sampling of "real-life" snowflake textures derived from Libbrecht's galleries (see Media and references below).

  I was able to implement several procedural generators using up to three random parameters. This randomness allows successive runs of the generators to produce unique flakes. These generators are artistic -- they don't follow ice symmetry or hold to realistic physical concepts of crystal formation.

  I've made some simplifying assumptions in designing the generators:

  • I use an accumlution buffer (2d texture) to store the integration.
  • the 2d texture is then translated into geometry via a vertex shader.

• for added realism, the snowflake is placed in an environment built from this skybox:


• I've also added a snowflake particle system for background effect.
• (not implemented) if there are distant lights, such as the sun, a snow halo and/or bloom effect (GLSL?) would be nice.

Original Storyboard and Concept

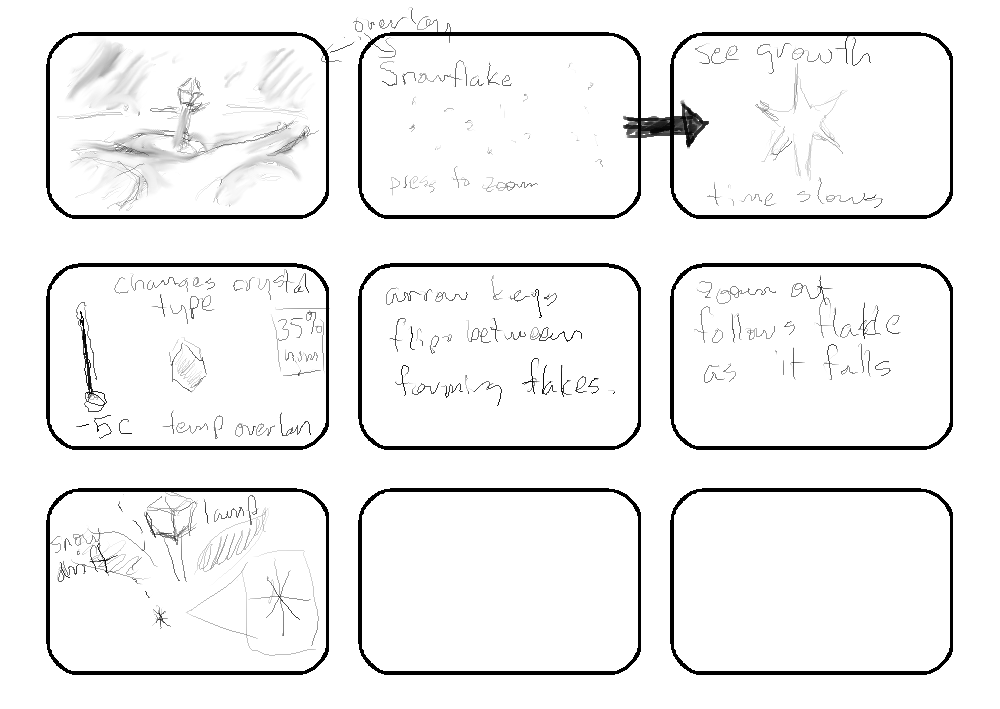
Frames:

1. (not implemented) The scene starts out with a lone lamp at a country path with snow drifts (the scene is surrounded with an environment map like the one above).
2. Overlayed on this is a 3D partical system of snow falling at normal speed (sprites or fuzzy points) and (not implemented) title graphics
3. (partially implemented) pressing a key focuses on a single point and time slows to microseconds so you can see the flake form from the point... the background is a diffuse gradient blend in order to see the polarization effects.
4. (implemented as 3 random params, but no controls) also available are temperature and humidity controls. varying these has an effect on what kind of flakes form, or the formation of existing flakes.
5. (different controls) arrow keys flip to another (new) flake, leaving the old one.
6. (not implemnted) user can also zoom out and see the flake fall to the ground, then hold on a long shot until the next flake zoom.

Image References:

• lamp in snow
• lamp post

OBJ file (courtesy of my sister Andrea who is an animator)

• (not implemented) This would need to be textured and placed in the scene.

Code

About the FBO textures

All snowflake generators are shapes rendered into an offscreen frame buffer object in GL_BLEND mode, and as such they accumulate any primatives rendered to the surface. Because the accumulated buffer is interpreted as a heightfield, these shapes also have depth.

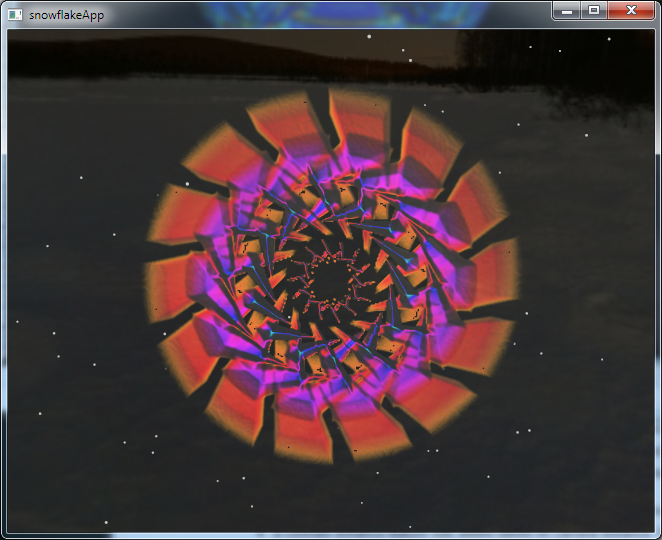
The generators have a prebuilt limit on the number of frames they are allowed to "grow". This is normalized in frame time to a range from 0 - 1.0 which then is used to define the radius of growth at a given frame time. This radius may then be multiplied times any of the random parameters, modulated, or otherwise transformed. In addition, a random number for the symmetry is chosen and any frame draw operations are rotated and repeated along these lines to produce a symmetrical effect.

I attempted another kind of generator using a Laplacian convolution filter (edge detection filter) under the idea that recursive applications of this filter would "grow" the edge of the snowflake. Indeed, I found out later that Laplacians are involved in actual diffusion physics, so this might have been a good approximation. I was planning to use this in combination with a hexagonal bias (like a lens flare) to encourage growth along symmetry lines. Although there are many examples of GLSL convolution filters, I couldn't get the shader to work in my specific context in time. Something for the future.

About the GLSL snowflake shader

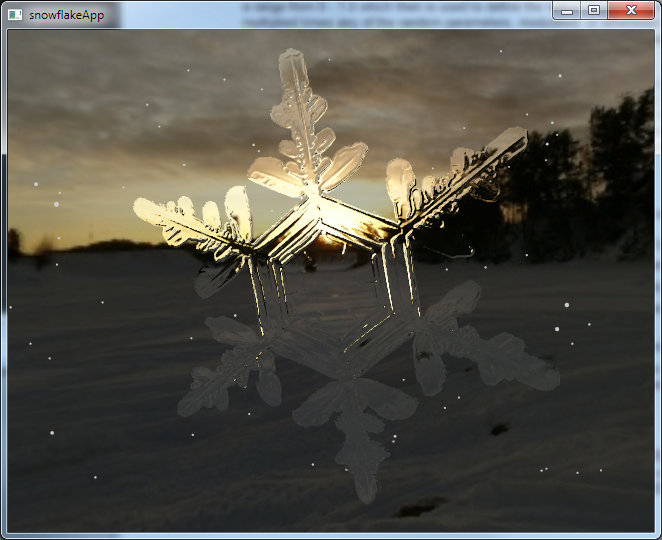
The snowflake GLSL shader does a combination of interesting things to achieve its effect.

• thickness is obtained from a greyscale frame buffer object (FBO) generated heightmap.
• thickenss is used for both the refraction effect and the thinfilm specular component.
• the "eta" (n1/n2) ratios for the index of refraction vary from 0.76 (ice) to 0.96 (almost air) based on the thickness.
• the refracted cubemap texel is blended with a non-refracted cubemap texel for thickness levels below a certain range... this cuts down on edge aliasing and gives a smoother image.
• the shader discards anywhere thickness = 0, this "cuts out" the snowflake from the square texture plate.
• a contrast enhance feature was added based on camera distance. far away, the flake is darkened a little and the surroundings are brightened a little. zooming in, this is reversed so that you can see the flake in better detail.

About the background snow flurry particle system

Snow particles use GL_POINTS along with the linear + exponential ATTENUATION parameter to generate larger points closer to the camera and smaller dots farther away. The particles have a downward impulse so they fall, and a xz impulse from a Perlin noise texture to simulate drifts and turbulence. I got the Perlin noise idea from Robert Hodgins particle system sample in the Cinder SDK. It's a simple precached way of generating psuedo turblence without CFDs.

About the controls and UI paradigm

The mouse controls for the camera rotation and object rotation are what I call a "ball on paper" model of interaction. Imagine a ball that has a center fixed in space that can rotate but not move. Now imagine that this ball rests on a sheet of paper on a desk. Moving your mouse on the screen (x,y) with a button down is akin to moving the paper. Moving the paper would rotate the ball about it's center.

This has a couple advantages over other approaches, such as "trackball" quaternion controls or raw euler angles:

• unlike "trackball" controls, it is possible to return exactly to a given orientation by simply returning to the same spot... this isn't possible in RenderMonkey or many other "trackball" implementations, which are very difficult to rotate and keep level at the same time.
• the "sheet of paper" is infinite, meaning that you can click, drag, release, and click again. This allows a long rotation to be broken up into smaller click-drag events, while still keeping an intuitive continuity.
• although euler angles are used in the implementation of this control system, the system itself avoids the common problem of gimbal lock by always maintaining a clean mapping between x and y accumulators. In the case of object rotation, the y axis rotation may not always be respective to the screen, but I thought this was a small price to pay for the overall consistency and simplicity of this approach.

The "real-life" snowflakes were produced via the following process using GIMP:

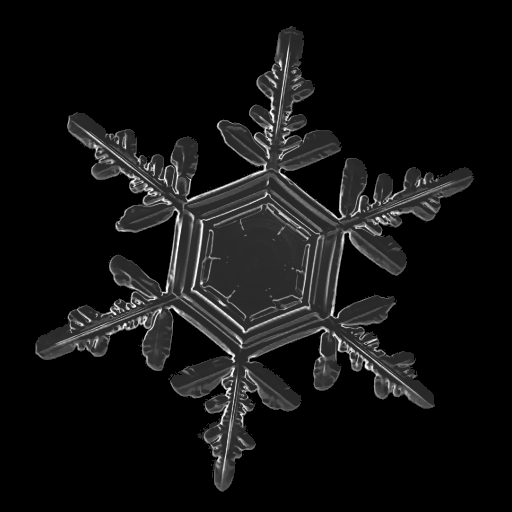
1. stock image selected from Libbrecht's collection
2. resize to 512x512
3. created a mask layer
4. desaturate: lightness
5. color: invert
6. levels: gamma = 0.35
7. brightness: +40
8. selective gaussian blur: 5.0 radius, 5 max delta.

Experience:

veteran multimedia systems and application programmer. (C++/Win32)

Target platform:

Windows 7 VS2010 C++ 32/64 bit

Libraries:

• Cinder C++ - a C++ library for creative coding; provides a lot of the "plumbing" needed for a typical OpenGL project. More modern than GLUT; cross platform support.
• For other media and asset licenses please see the included README.txt file.
• Also I reused concepts and code from our homeworks.

• This is a solo project because I'm an extension student.
• The features are laid out such that if I can't do one thing, I can fallback to another... so the scope of this can expand or contract as needed.

Kim, Theodore, Micheal Henson, and Ming C. Lin. "A Hybrid Algorithm for Modeling Ice Formation." UNC at Chapel Hill. 28 Nov. 2010. <http://gamma.cs.unc.edu/HYBICE/>.

Libbrecht, Kenneth. SnowCrystals.com. CalTech. 28 Oct. 2010. <http://www.its.caltech.edu/~atomic/snowcrystals/>.

---. "The physics of snow crystals." Reports on Progress in Physics. 68 (2005) 855-895. <http://www.its.caltech.edu/~atomic/publist/rpp5_4_R03.pdf>.

Wikipedia contributors, 'Procedural modeling', Wikipedia, The Free Encyclopedia, 4 August 2010, 01:29 UTC, <http://en.wikipedia.org/w/index.php?title=Procedural_modeling&oldid=377040651> [accessed 28 October 2010]

---, 'Thin-film interference', Wikipedia, The Free Encyclopedia, 29 September 2010, 02:33 UTC, <http://en.wikipedia.org/w/index.php?title=Thin-film_interference&oldid=387652589> [accessed 28 October 2010]